We investigate the existence of positive solutions for a class of fractional differential equations of arbitrary order δ2 subject to boundary conditions that include an integral operator of the fractional type. So we could call this a second order linear because A B and C definitely are functions just of-- well theyre not even functions of x or y theyre just constants.

Solution Of Differential Equations With Applications To Engineering Problems Intechopen

Introduction To Ordinary Differential Equations Coursera
Basic
Calculates the solution yfx of the ordinary differential equation yFxy using Runge-Kutta fourth-order method.

High order linear differential equations. In the first call to the function we only define the argument a which is a mandatory positional argumentIn the second call we define a and n in the order they are defined in the functionFinally in the third call we define a as a positional argument and n as a keyword argument. In partial differential equations they may depend on more than one variable. Introduction 2 videos First Order Equations 10 videos Second Order Equations 13 videos.
43 The Method of Undetermined Coefficients 181. The prerequisite for the course is the basic calculus sequence. Because such relations are extremely common differential equations have many prominent applications in real life and because we live in four dimensions these equations are often partial differential equations.
A firstorder differential equation is said to be homogeneous if M xy and N xy are both homogeneous functions of the same degree. The highest order of derivation that appears in a linear differential equation is the order of the equation. A differential equation that can be written in the form g y y f t or g y d y f t d t is called a separable differential equation.
In order to solve this polynomial equation we can use the Rational Root Theorem. Strangs textbook Differential Equations and Linear Algebra. The initial condition is y0fx0 and the root.
Answer to Solved 62. Differential equations relate a function with one or more of its derivatives. The term bx which does not depend on the unknown function and its derivatives is sometimes called the constant term of the equation by analogy with algebraic equations even when this term is a non-constant function.
Each Yi is found as a linear combination of the Fj added on to y0. Systems of Linear Equations Review for First Order Differential Equations Systems of Nonlinear Equations. So second order linear homogeneous-- because they equal 0-- differential equations.
This session consists of an imaginary dialog written by Prof. The classification of partial differential equations can be extended to systems of first-order equations where the unknown u is now a vector with m components and the coefficient matrices A ν are m by m matrices for ν 1 2 n. If all of the arguments are optional we can even call the function with no arguments.
This section aims to discuss some of the more important ones. And I think youll see that these in some ways are the most fun differential equations to solve. The parameter that will arise from the solution of this firstorder differential equation will be determined by the initial condition v0 v 1 since the sky divers velocity is v 1 at the moment the parachute opens and the clock is reset to t 0 at this instant.
A differential equation coupled with an initial value is called an initial-value problem. A first course on differential equations aimed at engineering students. The partial differential equation takes the form.
Special cases of the theorem are stated in Section 22 for separable equations Section 23 for linear equations and Section 24 for exact equations. 4 Higher-Order Linear Differential Equations 169. The differential equation is homogeneous because both M xy x 2 y 2 and N xy xy are homogeneous functions of the same degree namely 2.
Doing the same for first order nonlinear ODEs. Representing linear first order ODEs and Chao S. Topics include initial and boundary value problems.
Separation of variables for heat and wave equations on an interval and for Laplaces equation on rectangles and discs. 44 The Method of Variation of Parameters 185. Using the ode45 matlab to solve second order differential equations free online 7th grade text books How is doing operations adding subtracting multiplying and dividing with rational expressions similar to or different from doing operations with fractions.
In ordinary differential equations the functions u i must depend only on the single variable t. This video series develops those subjects both separately and together and supplements Prof. The video series is divided into eight parts corresponding to chapters of the textbook.
We will also discuss Clairauts Theorem to help with some of the work in finding higher order derivatives. In the section we will take a look at higher order partial derivatives. SECOND ORDER LINEAR ORDINARY DIFFERENTIAL EQUATIONS ODE 1 The ODE d²x dx m dt2 kt 0 dt describes a damped free oscillation of a mass m suspended on a spring with a positive damping constant and k the spring constant.
This free online book OER more formally should be usable as a stand-alone textbook or as a companion to a course using another book such as Edwards and Penney Differential Equations and Boundary Value Problems. According to this theorem if there is a rational root to a polynomial equation then that root must be in the form pq where p is a factor of the constant and q is the factor of the coefficient of the highest term. The consideration of this type of boundary conditions allows us to consider heterogeneity on the dependence specified by the restriction added to the equation as a relevant issue for.
NDSolve solves a wide range of ordinary differential equations as well as many partial differential equations. Their solutions LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION RETRIEVAL FROM NATURAL LANGUAGE TEXTS Quadratic Equations Syllabus for Differential Equations and Linear Alg Linear Equations and Matrices Solving Linear Equations. 5 Series Solutions of Second-Order Linear Equations 189.
Haynes Miller and performed in his 1803 class in spring 2010. 42 Homogeneous Differential Equations with Constant Coefficients 174. Computing and Modeling or Boyce and DiPrima.
Systems of first-order equations and characteristic surfaces. Unlike Calculus I however we will have multiple second order derivatives multiple third order derivatives etc. Wave and heat equations on the line half-line and in space.
If youre seeing this message it means were having trouble loading external resources on our website. First order linear and quasilinear equations method of characteristics. Eigenfunctions of the Laplacian and heat wave Poissons equations on bounded domains.
SECOND ORDER LINEAR ORDINARY DIFFERENTIAL. NDSolve can also solve many delay differential equations. Learn differential equations for freedifferential equations separable equations exact equations integrating factors and homogeneous equations and more.
Because we are now working with functions of multiple variables. 41 General Theory of n th Order Linear Differential Equations 169. It takes the form of a debate between Linn E.
Yi y0 h Xs j1 aijFj and the approximation at x1 x0 h is found from y1 y0 h Xs i1 biFi RungeKutta methods for ordinary differential equations p. The order of a differential equation is the highest order of any derivative of the unknown function that appears in the equation.

Figure 2 A Collocation Method Based On The Bernoulli Operational Matrix For Solving High Order Linear Complex Differential Equations In A Rectangular Domain

Solved Which Of The Following Is The General Solution Of High Order Second Neutra Linear Differential Equation With Constant Coefficients Whose Roots Are 5 71 1 0 5s 3 4 2q 0 C 0 Csin3r C Cos Ax A B 2q
Higher Order Linear Homogeneous Differential Equations With Constant Coefficients
Solved Second And High Order Linear Differential Equations Chegg Com

Pdf Laguerre Polynomial Solution Of High Order Linear Fredholm Integro Differential Equations Semantic Scholar
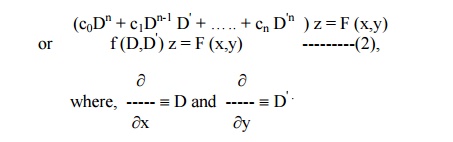
Partial Differential Equations Of Higher Order With Constant Coefficients

Differential Equation Wikipedia

Differential Equations Mathematics Mit Opencourseware


